Notion d'Arbre
Après les types abstraits linéaires, il est temps de commencer à parler arborescence et des arbres en informatique.
Pour commencer une petite video :
1 - L'Arbre en tant que type abstrait de données
Vous connaissez déjà ce type de structure.
Elle est assez courante dans la vie de tous les jours.
Ne serait-ce que par l'arbre généalogique.
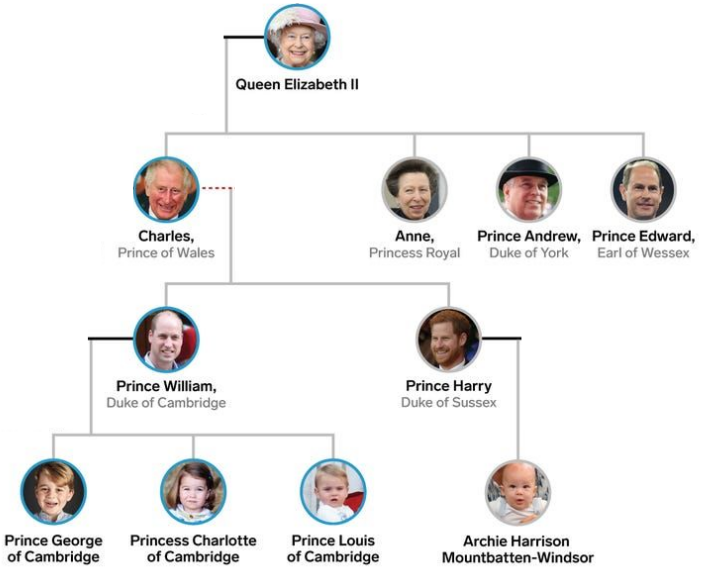
D'un point de vue informatique, l'arbre est présent un peu partout. Nous l'avons déjà rencontré l'année dernière lorsque nous avons parlé des balises HTML et de la structure que cela engendre : l'arbre DOM (pour Document Object Model).
Nous avions vu ce exemple de code HTML :
- La balise racine est la balise html. Elle contient :
- Une balise head
- Une balise body qui contient
- Une balise header qui contient d'autres balises...
- Une balise nav qui contient d'autres balises...
- Une balise main qui contient d'autres balises...
- Une balise footer qui contient d'autres balises...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40 | <!DOCTYPE html>
<html>
<head>
</head>
<body>
<header>
<h3>Le titre de mon site</h3>
</header>
<nav>
<ul>
<li>Accueil</li>
<li>Partie 1</li>
<li>Partie 2</li>
</ul>
</nav>
<main>
<h1>Le titre de ma page.</h1>
<h2>1 Première partie</h2>
<div>
<p>Bla bla.</p>
<p>Encore du Bla bla.</p>
<p>Toujours du Bla bla.</p>
</div>
<h2>2 Deuxième partie</h2>
<p>Encore du blabla.</p>
</main>
<footer>
<p>Pour contacter le webmaster, on met son adresse ici.</p>
<p>Pour l'instant, il préfère rester discret :</p>
<p>le contenu n'est pas très conséquent.</p>
</footer>
</body>
</html>
|
01° Imaginons que la structure HTML soit stockée dans une simple liste.
Pourrait-on trier les balises HTML entre elles pour les localiser plus facilement par dichotomie ?
Du coup, quel serait le coup d'une recherche pour par exemple trouver la balise <div> de la ligne 24 à la ligne 28 ?
...CORRECTION...
Difficile d'imaginer un classement performant des balises entre elles.
On pourra imaginer quelque chose comme associer chaque balise à un nombre en fonction de la balise qui la contient mais ça risque d'être vite assez complexe.
Du coup, pas de classement. Du coup, pas de dichotomie.
On revient à la recherche ligne par ligne, à coût linéaire donc.
Pourquoi dit-on que cette structure caractérise un arbre ?
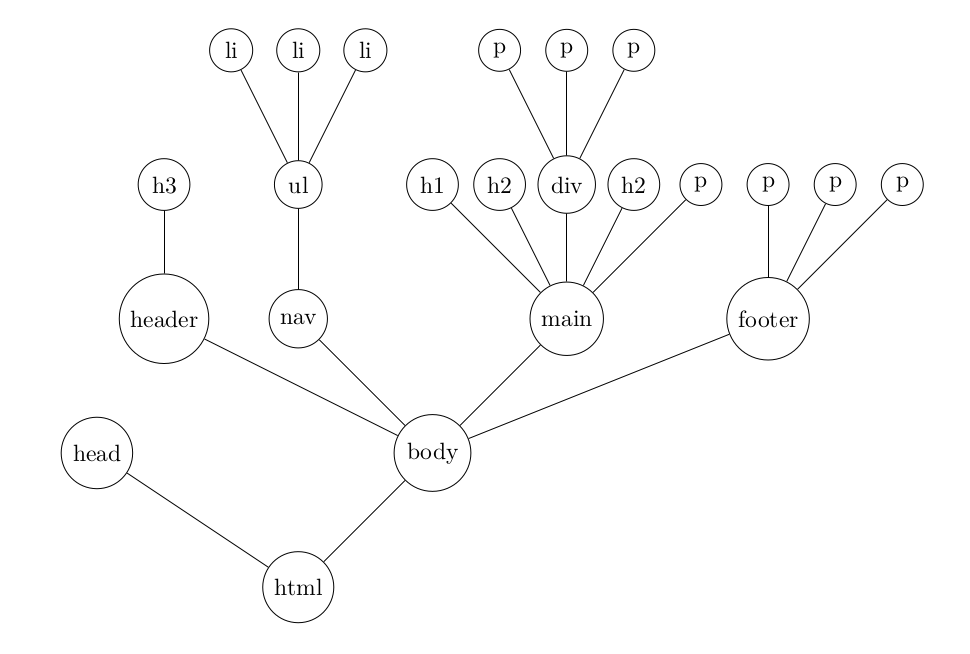
Visuellement, c'est clair : cela forme un arbre.
En revanche, attention :
nos arbres ne sont jamais tracés dans ce sens.
Contrairement aux vrais arbres, on a tendance à les dessiner avec la racine en haut et les feuilles en bas .
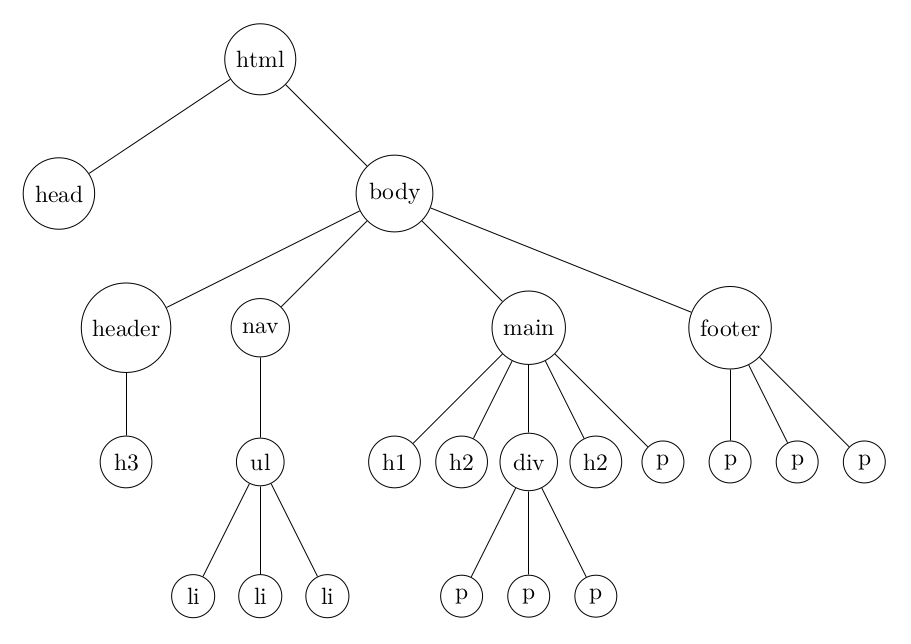
Si on parle en terme de recherche, vous imaginez bien que c'est très pratique de réflechir en terme d'arbre.
02° On cherche toujours la balise <div> contenue dans la balise main, elle-même contenue dans la balise body contenue dans html contenue dans ... Ah. Rien.
Partons de html qui joue un rôle particulier puisqu'elle n'est pas contenue dans une autre balise.
Combien de choix faire pour trouver notre balise div ?
...CORRECTION...
On part de la balise html, la racine et on voit qu'il faut partir vers la balise body. Ensuite, main. Et on localise notre balise div. 3 recherches donc.
.png)
Qu'est-ce qui n'est pas un arbre ?
Regardons déjà ce que n'est PAS un arbre :
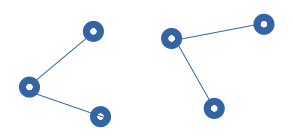
Exemple 1 : ceci n'est pas un arbre car on y trouve un cycle.
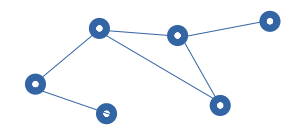
Exemple 2 : ceci n'est pas un arbre car l'objet obtenu n'est pas connexe : on trouve des couples de points sans chemin de l'un à l'autre.
Exemple 3 : ceci est un arbre mais on considèrera cette année qu'il manque encore une information. Laquelle ?
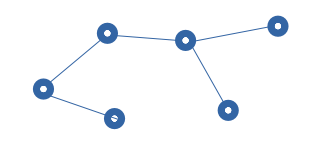
Les noeuds sont tous reliés entre eux (il y a un chemin possible entre tous les noeuds : on dit que l'arbre est connexe) mais il n'y a pas de cycle.
Il s'agit bien d'un arbre mais on se limite cette année aux arbres hierarchiques : il faut que l'un des sommets ai un rôle particulier qui nous permette de définir clairement ses propriétés. On nommera ce noeud la racine.
Si vous tombez sur une représentation de ce type, il suffit donc de choisir l'un des noeuds comme étant la racine.
En NSI, on n'abordera donc pas l'arbre non enraciné : nos arbres auront tous une racine , un noeud plus important que les autres.
1er partie de la définition du type abstrait de données ARBRE
Principe général d'organisation
Un arbre est un type abstrait de données ayant les propriétés suivantes (on parle ici des arborescences) :
- Il est composé de "cellules" qu'on nomme des noeuds contenant des informations dont
- Des données du type recherché (un nombre, un string...)
- Les liaisons éventuelles avec d'autres noeuds
- On hierarchise les noeuds entre eux : un noeud peut possèder
- un noeud-père (unique, un noeud ne peut pas posséder deux pères)
- un ou des noeuds-fils (un noeud peut avoir 0, 1 ou plusieurs fils)
- Racine : ce noeud UNIQUE est particulier car il est le seul noeud à ne pas possède de père. Il est tout en haut de la hierarchie.
- Feuille : il s'agit d'un noeud qui ne possède pas de fils. Il n'est pas unique. Un arbre peut possède plusieurs fils.
Un exemple tiré des noms de domaines (et du système DNS) :
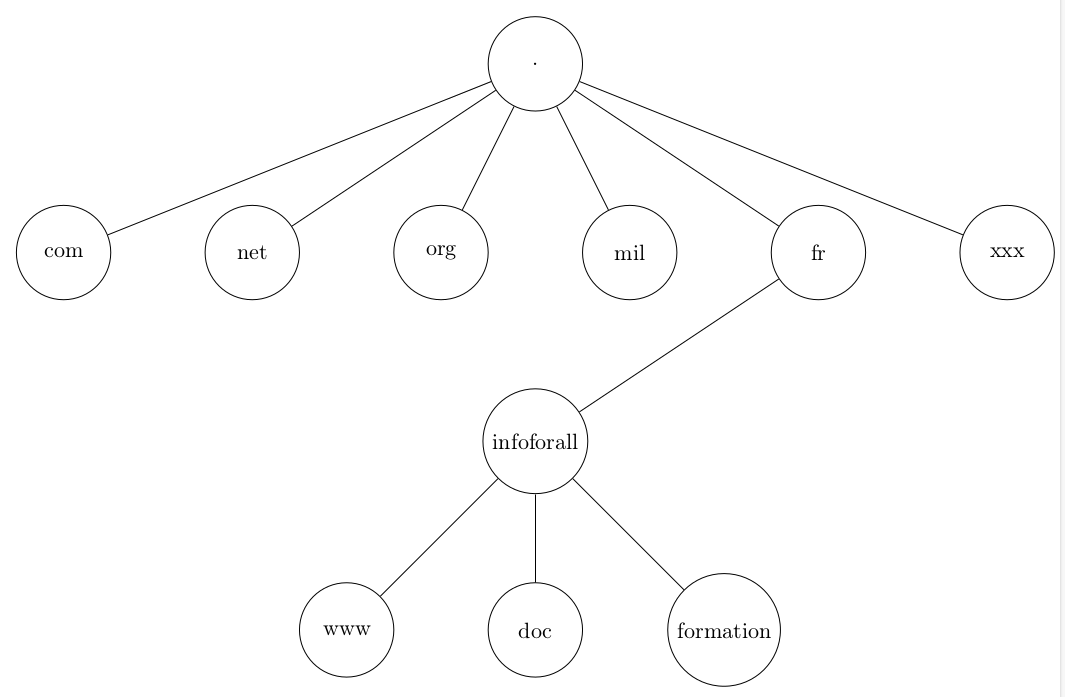
La RACINE se nomme point.
Cette racine possède 6 fils : com, net, org, mil, fr, xxx.
Le noeud fr possède un fils : inforall.
Le noeud infoforall possède trois fils : www, doc et formation.
Les feuilles sur cet arbre d'exemple sont com, net, org, mil, xxx, www, doc et formation.
Cet exemple vise à vous sensibiliser sur les choix de labels : deux noeuds peuvent ici très bien porter le même label. Mais dans une structure hierarchique de ce type, cela ne posera pas particulièrement de problème d'identification si on garde le nom du père par exemple.
Dans la liste chaînée, la recherche est à coût linéaire.
Définition récursive d'un arbre
On peut considérer qu'un arbre est composé
- soit d'un arbre vide
- soit de l'ensemble d'un noeud et des sous-arbres auxquelles il mène
03° Avec cette définition, peut-on considérer qu'un noeud peut avoir des fils "vides" ?
...CORRECTION...
Oui, un arbre-vide est un arbre. Un noeud n'ayant pas de fils (une feuille) est donc bien un arbre car on peut considérer que son "fils" mène à un arbre-vide qui est bien .. un arbre.
04° Combien d'arbres non vides dans cet arbre ?
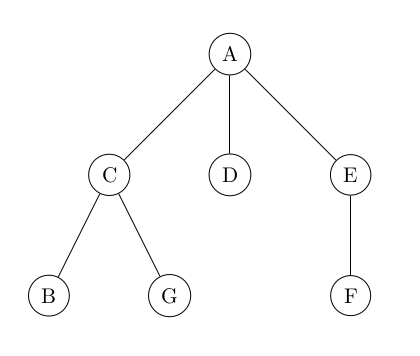
...CORRECTION...
7 arbres non vides.
05° Quelle est la racine cet arbre ? Quelles sont les feuilles de cet arbre ? Quels sont le ou les fils du noeud E ?
...CORRECTION...
06° Représentez l'arbre obtenu si on considère que la racine est maintenant le noeud D. Que pouvez-vous en dire au niveau d'une éventuelle localisation ?
...CORRECTION...
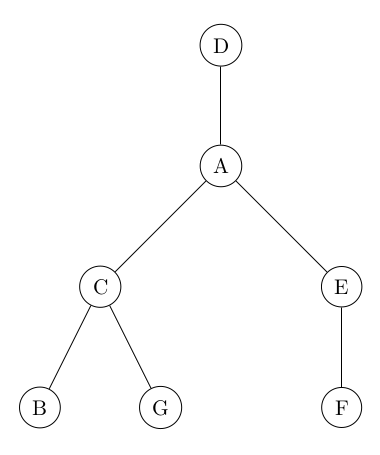
L'arbre est plus profond, il y aura plus de décisions à prendre. La racine précédente permettait une meilleur optimisation de la localisation.
Retenez bien que les arbres (ou arborescences) sont utilisés de façon massive en informatique et dans la vie de façon générale :
- système de fichiers des systèmes d'exploitation
- bases de données,
- documents structurés (HTML, XML),
- toutes les problèmes décisionnels non cycliques
Nous n'irons pas plus loin cette année avec l'arbre général.
Je ne donnerai pas les fonctions d'interface nécessaires à sa définition réelle.
Nous allons surtout nous concentrer sur un arbre particulier : l'arbre binaire.
2 - Arbre binaire
1er partie de la définition de l'arbre binaire
Un arbre binaire est composé
- La racine possède un fils gauche qu'on peut identifier comme tel (potentiellement un arbre vide donc)
- La racine possède fils droit qu'on peut identifier comme tel
La notion de distinction entre fils gauche et fils droit est fondamentale ici par rapport à l'arbre (arborescence) de la partie précédente.
On symbolise parfois l'arbre vide par un symbole particulier sur les arbres binaires : cela évite d'oublier un fils. Même si l'un des fils est un arbre-vide, il apparaît sur l'arbre.
Ici, nous avons deux arbres binaires différents, alors qu'en terme d'arborescence (l'arbre de la partie 1), c'est le même objet :
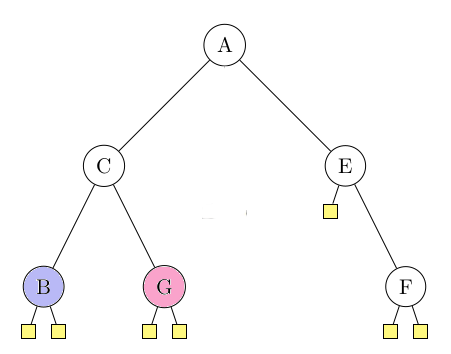
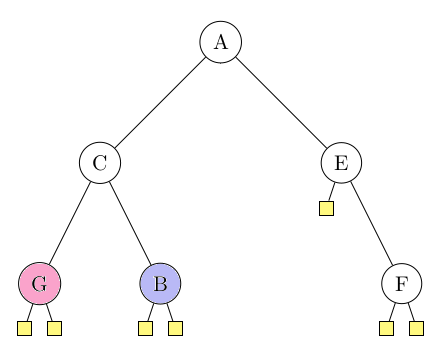
L'arbre binaire n'est pas identique car on identifie les fils gauche et droite.
VOCABULAIRE A MAITRISER : on notera
- qu'un noeud d'arbre binaire possède un fils gauche et un fils droit mais
- qu'un arbre binaire possède un sous-arbre gauche et un sous-arbre droit :
- Le fils gauche est donc la racine du sous-arbre gauche
- Le fils droit est donc la racine du sous-arbre droit
7° Expliquer si cet arbre est un arbre binaire ? Si l'arbre est binaire, noter les arbres vides non représentés sur l'arbre.
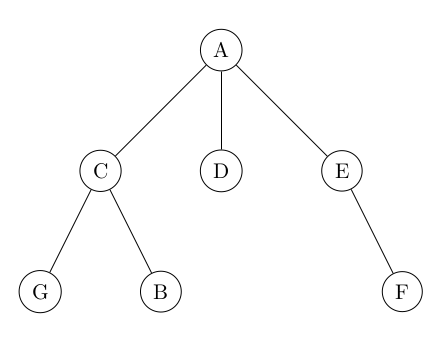
...CORRECTION...
Ce n'est pas un arbre binaire car le noeud A possède 3 fils.
8° Expliquer si cet arbre est un arbre binaire ? Si l'arbre est binaire, noter le symbole des arbres vides non représentés sur l'arbre.
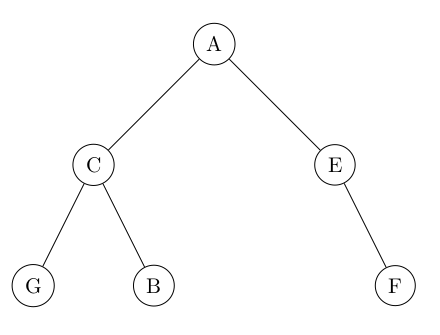
...CORRECTION...
Chaque noeud non vide possède bien deux fils : un fils gauche et un fils droite.
Certains fils sont des arbres-vides mais cela fait partie de la définition.
9° Entourer en rouge le sous-arbre gauche de l'arbre précédent. Entourer en bleu le sous-arbre droit. Entourer en vert le sous-arbre droit du sous-arbre gauche.
2e partie de la définition du type abstrait de données ARBRE BINAIRE : son interface
Description de l'interface minimale du type abstrait Arbre
Je le décris ici sous forme d'un type immutable, mais on pourait faire la même chose en non-mutable.
nvNd(x:Elt) -> Noeud: on crée un nouveau noeud et son élément attaché. Ce n'est pas une fonction d'interface de l'arbre mais on a besoin au moins de pouvoir créer un Noeud (les noeuds sont en même un type abstrait en réalité...)contenu(noeud:Noeud) -> Elt: renvoie l'élément (la valeur) contenue dans le noeud.nvAv() -> Arbre: on le note ainsi pour dire nvArbreBinaireVide : on crée un nouvel ARBRE BINAIRE vide.nvAB(noeud:Noeud, g:Arbre, d:Arbre) -> Arbre: on crée un nouvel ARBRE BINAIRE dont la racine est noeud et dont les sous-arbres sont g et d fournis.estArbreVide(arbre:Arbre) -> bool: True si l'arbre est un arbre vide.racine(arbre:Arbre) -> Noeud: renvoie le noeud jouant le rôle de la racine pour cet arbre.gauche(arbre:Arbre) -> Arbre: renvoie le sous-arbre gauche de arbre. On obtient bien un Arbre. Si vous voulez le noeud gauche, il faudra appliquer en plus la fonction racine.droite(arbre:Arbre) -> Arbre: renvoie le sous-arbre droit de arbre.
10° Créer l'arbre de la question 9 à l'aide de ces fonctions d'interface.
On considère que le contenu est juste un string portant le nom du noeud. Ainsi le noeud A porte l'information "A".
...CORRECTION...
a = nvNd('A')
b = nvNd('B')
c = nvNd('C')
e = nvNd('E')
f = nvNd('F')
g = nvNd('G')
arbre_F = nvAB(f, nvAv(), nvAv())
arbre_E = nvAB(e, nvAv(), arbre_F)
arbre_B = nvAB(b, nvAv(), nvAv())
arbre_G = nvAB(g, nvAv(), nvAv())
arbre_C = nvAB(c, arbre_G, arbre_B)
arbre_A = nvAB(a, arbre_C, arbre_E)
11° Utiliser les fonctions d'interface pour aller stocker dans valeur la valeur du noeud correspondant au fils-gauche de la racine de l'arbre.
On considère qu'on a accès initialement uniquement à la variable arbre qui fait référence à l'arbre de noeud A.
...CORRECTION...
arbre_g = gauche(arbre) # on récupère l'arbre_C en gros.
Pour récupérer la valeur, on fait :
c = racine(arbre_g) # on récupère le noeud C.
valeur = contenu(c) # on récupère la valeur associée à noeud C.
Ou en une étape :
valeur = contenu(racine(gauche(arbre)))
12° Utiliser les fonctions d'interface pour aller stocker dans reponse le fils droit du fils gauche de la racine.
Stocker alors sa valeur associée dans une variable valeur.
On considère qu'on a accès initialement uniquement à la variable arbre qui fait référence à l'arbre de noeud A.
...CORRECTION...
temp = gauche(arbre) # on récupère l'arbre_C en gros.
reponse = droite(temp) # on récupère l'arbre_B en gros.
Ou en une étape :
reponse = droite(gauche(arbre))
Pour récupérer la valeur, on fait :
b = racine(reponse) # on récupère le noeud B.
valeur = contenu(b) # on récupère la valeur associée à noeud B.
Ou en une étape :
valeur = contenu(racine(reponse))
3 - Caractéristiques des arbres binaires
Taille d'un arbre
La taille d'un arbre correspond au nombre de noeuds présents dans l'arbre.
On ne compte pas les arbres-vides : l'arbre-vide ne possède pas de noeud.
La taille de cet arbre est donc de 6.
Arête
Une arête est le segment qui relie deux noeuds.
Encore une fois, le terme est important : s'agissant de noeuds, on ne compte pas les "liaisons" entre un noeud et un fils-vide.
Ici, on compte donc 5 arêtes.
Profondeur d'un noeud
Il s'agit du nombre de noeud entre le noeud considéré et la racine.
Il existe ici deux écoles :
- Convention 1 : Soit on considère que la profondeur de la racine est de 1 : la racine est le premier étage de l'arbre.
- Convention 2 : Soit on considère que la profondeur de la racine est de 0 : la racine est le rez-de-chaussée, le niveau 0.
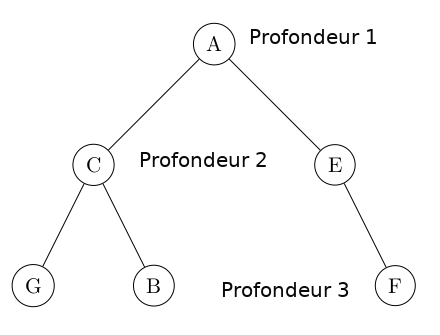
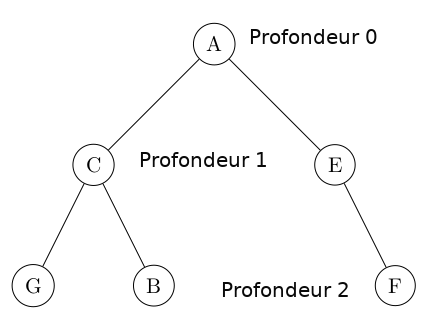
On vous indiquera le cas à respecter le jour du BAC. On vous dites clairement sur la copie la convention qui vous utilisez.
Propriété : quelque soit la convention choisie, la profondeur d'un noeud-fils est supérieure de 1 à celle de son père.
Propriété : si deux noeuds ont la même profondeur, c'est qu'ils sont à la même distance de la racine.
Hauteur d'un arbre
Il s'agit de la profondeur maximale qu'on trouve dans l'arbre, la "distance" entre la racine et la plus profonde des racines.
Moralité : ça dépend de la convention choisie pour trouver la profondeur.
- Convention 1 : Si la racine a une profondeur de 1, c'est pratique car un arbre-vide aurait une hauteur de 0. C'est "propre".
- Convention 2 : Si la profondeur de la racine est de 0, il suffit de considérer qu'un arbre-vide n'a pas de hauteur puisqu'il n'a pas de noeud et que la profondeur se mesure sur les noeuds. C'est "propre" aussi.
Sur cet exemple, la hauteur de l'arbre est donc de 3.
Sur cet exemple, la hauteur de l'arbre est donc de 2.
12° Fournir la taille, la hauteur et le nombre d'arêtes de cet arbre. Fournir également la profondeur du noeud C.
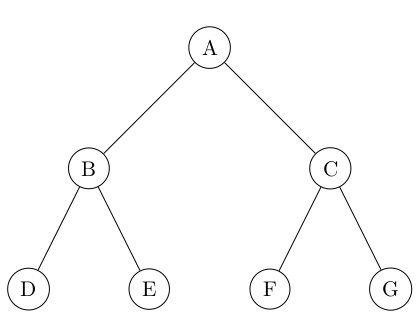
On dit que cet arbre est complet car la plus grande profondeur est intégralement composée de feuilles.
...CORRECTION...
13° Fournir la taille, la hauteur et le nombre d'arêtes de cet arbre. Fournir également la profondeur du noeud C.
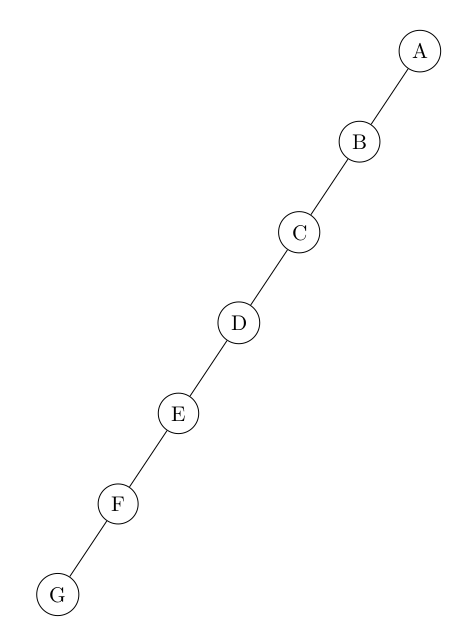
On parle d'arbre filiforme ou d'arbre dégénéré.
...CORRECTION...
14° Fournir la taille, la hauteur et le nombre d'arêtes de cet arbre. Fournir également la profondeur du noeud C.
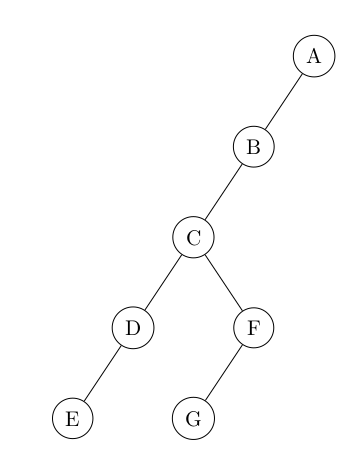
...CORRECTION...
15° Quelle va être la hauteur d'un arbre filiforme de taille n ?
...CORRECTION...
Si on considère une profondeur de 1 pour la racine, on obtient une hauteur de n.
Si on considère une profondeur de 0 pour la racine, on obtient une hauteur de n-1.
16° Calculer la taille d'un Arbre Complet dont on vous donne la hauteur (voir question 12) :
Si on considère une profondeur de 1 pour la racine :
- Hauteur h = 1 : Taille n = 1
- Hauteur h = 2 : Taille : n = 1 + 2 = 3
- Hauteur h = 3 : La taille : n = 1 + 2 + ...
- Hauteur h = 4 : La taille : n =
- Hauteur h = 5 : La taille: n =
Quelle fonction mathématique permettrait de trouver la hauteur h connaissant la taille n de l'arbre complet ?
Si on considère une profondeur de 0 pour la racine :
- Hauteur h = 0 : Taille n = 1
- Hauteur h = 1 : Taille : n = 1 + 2 = 3
- Hauteur h = 2 : La taille : n = 1 + 2 + ...
- Hauteur h = 3 : La taille : n =
- Hauteur h = 4 : La taille: n =
Quelle fonction mathématique permettrait de trouver la hauteur h connaissant la taille n de l'arbre complet ?
...CORRECTION...
Profondeur de 1 pour la racine
- Hauteur h = 1 : Taille n = 1
- Hauteur h = 2 : Taille n = 1 + 2 = 3
- Hauteur h = 3 : Taille n = 1 + 2 + 4 = 7
- Hauteur h = 4 : Taille n = 1 + 2 + 4 + 8 = 15
- Hauteur h = 5 : Taille n = 1 + 2 + 4 + 8 + 16 = 31
On remarque qu'on peut écrire
n + 1 = 2h ( formule 2-R1 )
Si on passe par le log2 de chaque côté :
log2(n+1) = log2(2h)
On peut donc en déduire que pour un arbre binaire complet (avec une racine de profondeur 1):
log2(n+1) = h
Au final, en présentant la hauteur d'abord :
h = log2(n+1) ( formule 1-R1 )
Profondeur de 0 pour la racine
- Hauteur h = 0 : Taille n = 1
- Hauteur h = 1 : Taille n = 1 + 2 = 3
- Hauteur h = 2 : Taille n = 1 + 2 + 4 = 7
- Hauteur h = 3 : Taille n = 1 + 2 + 4 + 8 = 15
- Hauteur h = 4 : Taille n = 1 + 2 + 4 + 8 + 16 = 31
On remarque qu'on peut écrire
n + 1 = 2h+1 ( formule 2-R0 )
Si on passe par le log2 de chaque côté :
log2(n+1) = log2(2h+1)
On peut donc en déduire que pour un arbre binaire complet (avec une racine de profondeur 1):
log2(n+1) = h + 1
log2(n+1) - 1 = h
Au final, en présentant d'abord la hauteur :
h = log2(n+1) - 1 ( formule 1-R0 )
On retiendra donc qu'on peut trouver la hauteur h d'un Arbre Binaire de taille n à l'aide de la fonction logarithme 2.
Encadrements de la hauteur d'un Arbre Binaire
Les deux cas extrêmes étant :
- Arbre binaire filiforme
- Arbre binaire complet
On en déduit que pour un arbre binaire quelconque, situé entre ces deux cas particuliers extrêmes, on peut encadrer la hauteur de l'arbre binaire quelconque à l'aide de la formule suivante :
Encadrement avec une profondeur 1 pour la racine :
⌈log2(n+1)⌉ ≤ h ≤ n
On notera que les signes ⌈ ⌉ indiquent simplement un arrondi à l'entier supérieur.
Encadrement avec une profondeur 0 pour la racine
⌊log2(n)⌋ ≤ h ≤ n - 1
Cette fois, les signes ⌊ ⌋ veulent dire d'arrondir à l'inférieur.
Exemple : un arbre binaire complet de 15 noeuds possède une hauteur de 4 si la racine a une profondeur de 1.
Si on tape ceci dans Python,
>>> import math
>>> math.log2(15+1)
4.0
>>> math.log2(16+1)
4.087462841250339
On voit alors qu'un arbre de 15 noeuds à une hauteur comprise dans [4; 15].
Par contre, avec 16 noeuds, on obtient une hauteur comprise dans [5;16].
C'est normal : avec 15 noeuds, l'arbre serait complet dans le meilleur des cas. Si on en rajoute un, il faut nécessairement rajouter un étage...
4 - FAQ
Pourquoi on arrondit à l'inférieur dans le cas de l'encadrement avec une profondeur de 0 pour la racine ?
La formule reliant h et n d'un Arbre Binaire Complet pour cette profondeur est :
h = log2(n+1) - 1 ( formule 1-R0 )
On pourrait donc écrire ceci :
⌈log2(n+1)⌉ - 1 ≤ h ≤ n - 1
On peut obtenir le même résultat en arrondissant simplement à l'inférieur du coup :
⌊log2(n)⌋ ≤ h ≤ n - 1
C'est quoi l'arité ?
C'est le nombre de fils maximum qu'un noeud peut avoir.
Si un arbre est d'arité 2, cela veut donc dire qu'aucun noeud de cet arbre n'a trois fils.
Un arbre classique d'arité 2 implique que les noeuds peuvent avoir 0, 1 ou 2 noeuds-fils.
Un arbre binaire est d'arité 2 puisque chaque noeud mène à deux sous-arbre gauche et droite, même s'ils sont des arbres vides !
C'est quoi le degré d'un noeud ?
Il s'agit tout simplement du nombre de liaison que possède le noeud.
Voir le cours sur les graphes, les arbres pouvant être vus comme un cas particulier des graphes.
J'ai vu un cours avec une hauteur pour un noeud, c'est normal ?
Et oui, il n'y a pas que la racine qui possède une hauteur.
La profondeur d'un noeud est un nombre représentant la "distance" entre la racine et ce noeud.
La hauteur d'un noeud est la "distance" entre le noeud et la racine la plus éloignée dans son sous-arbre.
Et on ne peut pas encadrer la taille n connaissant h ?
Si, mais c'est dans une autre activité.
On obtient ceci :
Encadrement de la taille n dans le cas profondeur de racine 1 :
h ≤ n ≤ 2h - 1
Encadrement de la taille n dans le cas profondeur de racine 0 :
h + 1 ≤ n ≤ 2h+1 - 1
Activité publiée le 04 02 2021
Auteur : Andjekel
Sources : Infoforall et NSI4NOOBS