Arbre Binaire de Recherche
Nous avons vu que la recherche dans un Arbre Binaire était plus efficace lorsqu'on sait où chercher.
Le coût est alors fonction de la hauteur h de l'Arbre Binaire : θ(h). Du coup,
On rappelle les notations utilisées pour les algorithmes en pseudo langage :
Soit un arbre T : T.racine correspond au noeud racine de l'arbre T
Soit un noeud x :
- x.gauche correspond au sous-arbre gauche du noeud x
- x.droit correspond au sous-arbre droit du noeud x
- x.clé correspond à la clé du noeud x
Il faut noter que si le noeud x est une feuille, x.gauche et x.droite sont des arbres vides (NIL)
Nous allons voir aujourd'hui un Arbre conçu spécifiquement pour pouvoir savoir où chercher la clé qui nous intéresse.
Prérequis :
- Données : Arbre et Arbre Binaire
- Algos : Parcours d'Arbres
- Algos : Algorithmes des Arbres Binaires
1 - Arbre Binaire de Recherche (ABR)
Définition d'un Arbre Binaire de Recherche
Un Arbre Binaire de Recherche est un Arbre Binaire qui respecte une organisation ordonnéee particulière.
Les Clés des Noeuds doivent toutes pouvoir être comparées entre elles (c'est à dire disposer d'un opérateur < ou > ...).
La définition de l'Arbre Binaire de recherche impose que :
- Toutes les clés du sous-arbre gauche sont plus petites* que la clé de la racine de l'Arbre étudié
- Toutes les clés du sous-arbre de droite sont plus grandes* que la clé de la racine de l'Arbre étudié
La présence du * indique que l'égalité peut être traitée comme vous le voulez : à vous de choisir si vous voulez insérer un tel noeud à droite ou à gauche.
Dans un premier temps, nous nous limiterons au cas des arbres pour lequel les clés sont toutes différentes.
Exemples
Un Arbre Binaire de Recherche Complet :
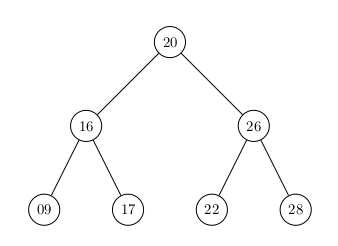
Les mêmes noeuds avec les mêmes clés dans une configuration moins optimale pour la recherche :
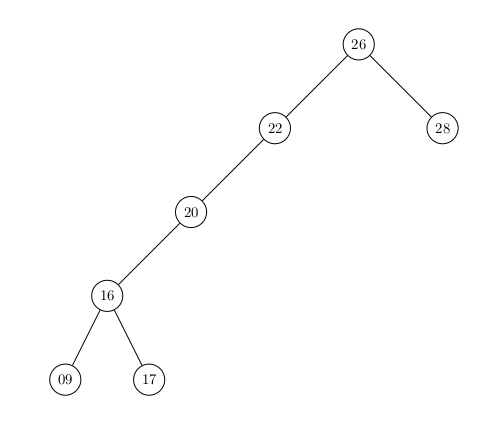
L'intérêt ?
Comme pour la liste-tableau trié qui permet une recherche dichotomique à coût logarithmique plutôt que linéaire,
l'ABR permet une recherche à coût logarithmique (sur un Arbre proche d'un Arbre Complet) plutôt que linéaire.
En Anglais
En anglais, on dit Binary Search Tree ou BST.
Et maintenant une petite video :
Pour l'instant la regarder jusqu'au début du programme python
01° Vérifier que toutes les clés à gauche du Noeud de clé 20 sont inférieures à 20 et que tous les Noeuds dont la clé est supérieure à 20 est dans le sous-arbre droite de l'arbre de racine 20.

02° Créer un nouvel Arbre Binaire de Recherche (ABR) un peu moins optimisé pour la recherche mais comportant les mêmes clés : le noeud-père du Noeud de clé 17 est directement le Noeud de clé 20.
Trouver deux versions du sous-arbre gauche possibles.
Pourquoi cet Arbre est-il moins optimisé pour la recherche ?
...CORRECTION...
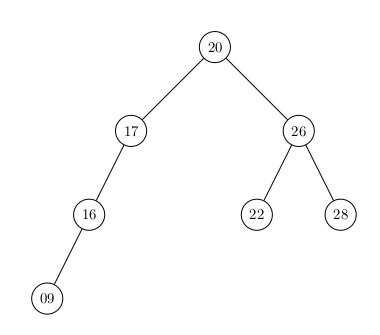
Ou encore
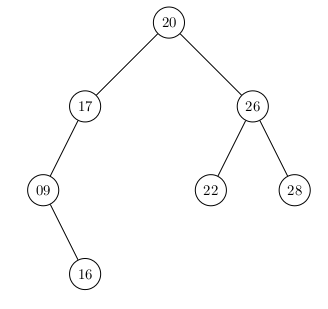
Il est moins optimisé que l'Arbre Binaire Complet puisqu'il possède un étage en plus : la recherche du noeud de clé 9 sera plus longue d'une étape.
Création progressive d'un ABR
On commence par la racine puis on positionne progressivement les autres éléments, un à la fois.
Pour rajouter les noeuds (dont on connaît la clé) proposés, on suit ce principe :
- Partir de la racine
- Si la clé à placer est inférieure à celle du noeud actuel, on place la clé à gauche si le sous-arbre gauche est vide, sinon on répète l'opération en partant de la racine du sous-arbre gauche.
- Si la clé à placer est supérieure ou égale à celle du noeud actuel, on place la clé à droite si le sous-arbre droite est vide, sinon on répète l'opération en partant de la racine du sous-arbre droite.
Exemple
On part de 50 et on rajoute 30.
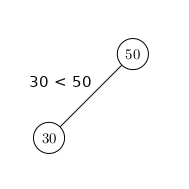
On rajoute ensuite 45.
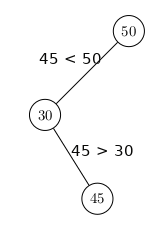
Puis 65.
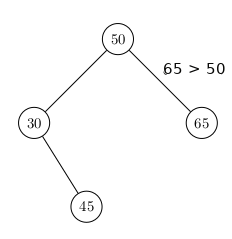
Puis éventuellement à nouveau 65.
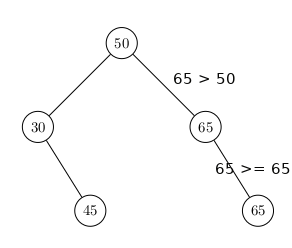
On notera donc qu'il faut faire très attention au cas des ABR lorsque des noeuds peuvent porter la même clé. Il existe des algorithmes d'insertion plus performants qui permettent de limiter la hauteur des AB si on rajoute plusieurs fois des clés identiques. On ne s'en préoccupera pas cette année.
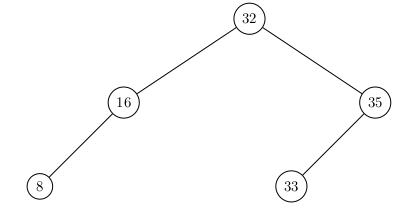
04° Créer un nouvel Arbre Binaire de Recherche (ABR) dont les clés suivantes sont insérées progressivement : 32-16-8-35-33.
...CORRECTION...
05° Même question en modifiant la place du 35 : 35-32-16-8-33.
L'ordre d'apparition des clés est-elle importante avec ce principe d'insertion ?
...CORRECTION...
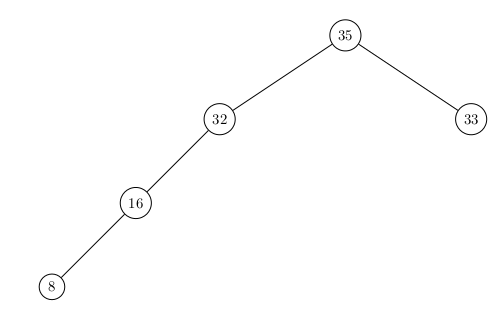
L'ordre des clés est effectivement à surveiller : on n'obtiendra pas le même arbre avec une séquence différente.
2 - Algorithme d'insertion
Nous allons maintenant voir comment réaliser avec un algorithme ce que vous avez fait juste au dessus.
La différence fondamentale avec les petits exercices ci-dessus est qu'on va chercher à insérer un Noeud qui possède une Clé ainsi que d'autres données éventuelles, et pas à insérer un Noeud créé pour l'occasion et ne contenant que la Clé.
Un algorithme d'insertion dans un arbre binaire de recherche (non vide)
Un exemple
Nous Allons créer un algorithme avec les fonctions d'interface (ou primitives) vues précédemment mais également de deux nouvelles fonctions permettant d'insérer un nouvel Arbre Binaire de Recherche à gauche ou à droite :
Les fonctions liées aux Noeuds :
nvND(cle:Cle, data:Data) -> Noeud: on crée un nouveau noeud et son élément attaché. Ce n'est pas une fonction d'interface de l'arbre mais on a besoin au moins de pouvoir créer un Noeud.cle(noeud:Noeud) -> Cle: renvoie la clé ou l'étiquette du noeud.data(noeud:Noeud) -> Data: renvoie les données associées au noeud.
Les fonctions liées à l'Arbre Binaire de Recherche lui-même :
nvAV() -> Arbre: on le note ainsi pour dire nouvelArbreVide : on crée un nouvel ARBRE BINAIRE vide.nvABR(r:Noeud, g:Arbre, d:Arbre) -> Arbre: on crée un nouvel ARBRE BINAIRE de RECHERCHE dont la racine est r et dont les sous-arbres sont g et d fournis.estArbreVide(arbre:Arbre) -> bool: True si l'arbre est un arbre vide.racine(arbre:Arbre) -> Noeud: renvoie le noeud jouant le rôle de la racine pour cet arbre.gauche(arbre:Arbre) -> Arbre: renvoie le sous-arbre gauche de arbre. On obtient bien un Arbre. Si vous voulez le noeud gauche, il faudra appliquer en plus la fonction racine.droite(arbre:Arbre) -> Arbre: renvoie le sous-arbre droit de arbre.inserer_gauche(arbre:Arbre, g:Arbre) -> None: on remplace le sous-arbre gauche de arbre par l'arbre g.inserer_droite(arbre:Arbre, d:Arbre) -> None: on remplace le sous-arbre droite de arbre par l'arbre d.
Les deux nouvelles fonctions liées à l'insertion :
Regardons maintenant comment traduire l'insertion sous forme d'un algorithme.
L'algorithme proposé consiste à mémoriser la position en cours (dans arbre) et la position de l'étape précédente (dans arbre_parent).
Algorithme d'insertion d'un noeud dans un Arbre Binaire de Recherche NON VIDE
ENTREE 1 : l'ABR arbre (non vide) avec lequel on veut travailler
ENTREE 2 : le noeud nd (possèdant une clé c et des données annexes éventuelles) qu'on veut rajouter à notre arbre.
SORTIE : Vide, on modifie ici l'arbre sur place
inserer_noeud_dans_ABR(arbre:ABR, nd:Noeud) -> Vide
étape 1 : on crée arbre_parent, variable qui va contenur la référence de l'arbre où insérer le Noeud nd
arbre_parent ← Vide
étape 2 : on explore l'arbre jusqu'à trouver la bonne position
TANT QUE NON estArbreVide(arbre)
arbre_parent ← arbre
SI cle(nd) < cle(racine(arbre))
arbre ← gauche(arbre)
SINON
arbre ← droite(arbre)
Fin SI
Fin Tant Que
étape 3 : on insère l'arbre dont nd est la racine au bon endroit
SI cle(nd) < cle(racine(arbre_parent))
inserer_gauche(arbre_parent, nvABR(nd, nvAV(), nvAV()) )
SINON
inserer_droite(arbre_parent, nvABR(nd, nvAV(), nvAV()) )
Fin SI
Renvoyer VIDE
06° Quels sont les coûts des étapes 1, 2 et 3 ? Quel est le coût de l'insertion d'un nouveau noeud dans un ABR (par rapport à la hauteur de l'ABR) ?
...CORRECTION...
Etape 1 : Coût constant θ(1).
Etape 2 : Coût linéaire en fonction de la hauteur h de l'arbre dans le pire des cas θ(h).
Etape 3 : Coût constant θ(1).
Au total, l'insertion est donc LINEAIRE par rapport à la hauteur h de l'ABR.
07° Exécuter l'algorithme pour insérer 31 dans cet Arbre :
Que contiennent les clés des racines de arbre_parent et arbre à chaque tour dans la boucle TANT QUE puis à la fin de l'algorithme ?
...CORRECTION...
On commence par une racine vide pour arbre_parent et une clé 33 pour arbre.
Ensuite, on rentre dans la boucle TANT QUE.
1er tour de boucle :
- arbre_parent possède la clé 33
- arbre possède la clé 16
1er tour de boucle :
- arbre_parent possède la clé 16
- arbre possède la clé 32
3e tour de boucle :
- arbre_parent possède la clé 32
- arbre ne possède pas de clé car il fait référence à un arbre vide
On sort donc de la boucle.
A la fin des boucles, on voit donc qu'on va insérer le nouveau noeud sur le noeud-parent 32 puisque arbre_parent possède la clé 32.
Coût de l'insertion dans un Arbre Binaire de Recherche
Le coût est fonction de la hauteur h l'Arbre Binaire : θ(h). Du coup,
- Si l'AB est complet, on obtient alors un coût logarithmique sur la taille de l'Arbre :
θ(log2(n)) - Si l'AB est filiforme, on retrouve juste un coût linéaire par rapport à la taille :
θ(n) - Si l'AB est quelconque, on est entre les deux.
3 - Algorithme de recherche
Comme nous l'avons vu, il est facile de trouver la prochaine étape lorsqu'on cherche une clé dans un ABR : on compare la clé cherchée avec la clé du noeud actuel, et on sait si on doit aller à droite ou à gauche. L'Arbre Binaire de Recherche permet donc de faire des ... recherches ciblées. C'est le but. Nous allons donc retrouver le fait que :
Coût de la recherche dans un Arbre Binaire de Recherche
Le coût est alors fonction de la hauteur h l'Arbre Binaire : θ(h). Du coup,
- Si l'AB est complet, on obtient alors un coût logarithmique sur la taille de l'Arbre :
θ(log2(n)) - Si l'AB est filiforme, on retrouve juste un coût linéaire par rapport à la taille :
θ(n) - Si l'AB est quelconque, on est entre les deux.
Un algorithme de recherche d'une clé dans un arbre binaire de recherche (ABR)
Nous allons maintenant étudier un algorithme permettant de rechercher une clé de valeur k dans un arbre binaire de recherche.
Si k est bien présent dans l'arbre binaire de recherche, l'algorithme renvoie vrai, dans le cas contraire, il renvoie faux.
VARIABLE
T : arbre
x : noeud
k : entier
DEBUT
ARBRE-RECHERCHE(T,k) :
si T == NIL :
renvoyer faux
fin si
x ← T.racine
si k == x.clé :
renvoyer vrai
fin si
si k < x.clé :
renvoyer ARBRE-RECHERCHE(x.gauche,k)
sinon :
renvoyer ARBRE-RECHERCHE(x.droit,k)
fin si
FIN
Cet algorithme de recherche d'une clé dans un arbre binaire de recherche ressemble beaucoup à la recherche dichotomique vue en première dans le cas où l'arbre binaire de recherche traité est équilibré.
La complexité en temps dans le pire des cas de l'algorithme de recherche d'une clé dans un arbre binaire de recherche équilibré est donc O(log2(n)).
Dans le cas où l'arbre est filiforme, la complexité est O(n).
Rappelons qu'un algorithme en O(log2(n)) est plus "efficace" qu'un algorithme en O(n).
À noter qu'il existe une version dite "itérative" (qui n'est pas récursive) de cet algorithme de recherche :
08° En utilisant les fonctions d'interfaces vues précédemment, proposer un algorithme permettant de rechercher un noeud dans un ABR.
On travaillera à partir des indications ci-dessous :
Dans un Arbre Binaire de Recherche, la recherche d'une Clé cr est ciblée : inutile de faire une recherche linéaire en profondeur ou en largeur. Il suffit de comparer la valeur de la clé cr cherchée et la valeur de la clé c du noeud actuel pour savoir où aller ensuite.
- Si l'arbre actuel est un arbre vide, on renvoie une réponse VIDE.
- Si c'est la bonne clé (
cr == c), on a trouvé. On renvoie alors le Noeud de la racine de l'arbre actuel. - Si la clé cherchée est plus petite que la clé du noeud (
cr < c): on va à gauche. - Si la clé cherchée est plus grande que la clé du noeud (
cr > c): on va à droite.
Algorithme de recherche
ENTREE 1 : un Arbre Binaire de Recherche arbre
ENTREE 2 : une Clé cr
SORTIE : la référence d'un Noeud portant cette clé ou VIDE
recherche(arbre:ABR, cr:Cle) -> Noeud|Vide
A vous d'agir !
Algorithme de recherche dans un ABR : version itérative en utilisant l'interface
Dans un Arbre Binaire de Recherche, la recherche d'une Clé cr est ciblée : inutile de faire une recherche linéaire en profondeur ou en largeur. Il suffit de comparer la valeur de la clé cr cherchée et la valeur de la clé c du noeud actuel pour savoir où aller ensuite.
- Si l'arbre actuel est un arbre vide, on renvoie une réponse VIDE.
- Si c'est la bonne clé (
cr == c), on a trouvé. - Si la clé cherchée est plus petite que la clé du noeud (
cr < c): on va à gauche. - Si la clé cherchée est plus grande que la clé du noeud (
cr > c): on va à droite.
Algorithme de recherche
ENTREE 1 : un Arbre Binaire de Recherche arbre
ENTREE 2 : une Clé cr
SORTIE : la référence d'un Noeud portant cette clé
recherche(arbre:ABR, cr:Cle) -> Noeud
TANT QUE NON estArbreVide(arbre)
SI cr == cle(racine(arbre))
Renvoyer racine(arbre)
SINON SI cr < cle(racine(arbre))
arbre ← gauche(arbre)
SINON SI cr > cle(racine(arbre))
arbre ← droite(arbre)
Fin SI
Fin Tant Que
Renvoyer VIDE
09° Appliquer cet algorithme sur cet arbre en cherchant 22.

10° Dans le pire des cas, quel est le coût de cet algortihme en fonction de la hauteur de l'arbre ? En fonction de la taille pour un arbre complet ?

...CORRECTION...
On retrouve un coût linéaire par rapport à la hauteur.
Pour un arbre complet, le coût est donc logarithmique base 2 par rapport à la taille puisqu'à chaque étape, on réduit approximativement par deux le nombre de noeuds à supprimer de la recherche.
Pour Information : ABR complet et ABR équilibré
Vous savez maintenant qu'un ABR est complet si le dernier étage est composé uniquement des feuilles de l'arbre.

Nous venons de voir que dans ce cas, le coût de l'insertion et de la recherche est θ(log2(n)).
Or, ce cas est assez rare cas il faut déjà au moins que le nombre de noeuds soit égal à une puissance de 2 moins 1 : n = 2x - 1.
La notion d'arbre équilibré possède plusieurs variantes.
L'important est de comprendre qu'il s'agit d'un arbre pour lequel les recherches peuvent toutes se ramener à peu près au cas de l'arbre complet.
C'est le "à peu près" qui fera la différence entre les définitions.
En 1962 que deux Russes, Adel'son-Vel'skii et Landis, introduisent des critères définissant un équilibre.
Les arbres vérifiant ces critères sont connus sous le nom d'arbres AVL. Avec ce critère AVL, pour tout nœud de l'arbre, la différence entre les hauteurs de ses deux fils ne peut excéder 1..
Cet Arbre n'est pas un Arbre Binaire équilibré (je considère une hauteur de 0 pour une racine seule)
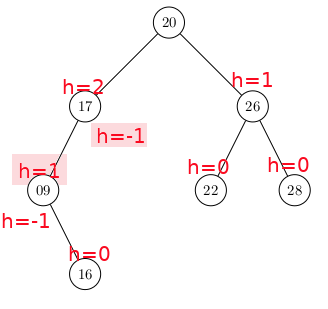
Par contre, cet Arbre est un Arbre Binaire équilibré :
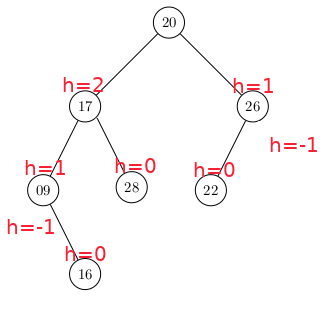
Pour un Arbre Binaire équilibré, on considère que le coût d'une recherche ou d'une insertion est au pire logarithmique par rapport à la taille de l'arbre (θ(log2(n))).
4 - FAQ
Arbre binaire de recherche et parcours infixe
Il est important de noter qu'un parcours infixe d'un arbre binaire de recherche permet d'obtenir les valeurs des noeuds de l'arbre binaire de recherche dans l'ordre croissant.
Les fonctions d'interface courantes d'un ABR (primitives)
Les fonctions liées aux Noeuds :
nvND(cle:Cle, data:Data) -> Noeud: on crée un nouveau noeud et son élément attaché. Ce n'est pas une fonction d'interface de l'arbre mais on a besoin au moins de pouvoir créer un Noeud.cle(noeud:Noeud) -> Cle: renvoie la clé ou l'étiquette du noeud.data(noeud:Noeud) -> Data: renvoie les données associées au noeud.
Les fonctions liées à l'ABR lui-même :
nvAV() -> Arbre: on le note ainsi pour dire nouvelArbreVide : on crée un nouvel ARBRE BINAIRE vide.nvAB(r:Noeud, g:Arbre, d:Arbre) -> Arbre: on crée un nouvel ARBRE BINAIRE dont la racine est r et dont les sous-arbres sont g et d fournis.estArbreVide(arbre:Arbre) -> bool: True si l'arbre est un arbre vide.racine(arbre:Arbre) -> Noeud: renvoie le noeud jouant le rôle de la racine pour cet arbre.gauche(arbre:Arbre) -> Arbre: renvoie le sous-arbre gauche de arbre. On obtient bien un Arbre. Si vous voulez le noeud gauche, il faudra appliquer en plus la fonction racine.droite(arbre:Arbre) -> Arbre: renvoie le sous-arbre droit de arbre.inserer_gauche(arbre:Arbre, g:Arbre) -> None: on remplace le sous-arbre gauche de arbre par l'arbre g.inserer_droite(arbre:Arbre, d:Arbre) -> None: on remplace le sous-arbre droite de arbre par l'arbre d.recherche(arbre:ABR, cr:Cle) -> Noeudparent(arbre:Arbre) -> Arbre: renvoie le parent de arbre si il existe.
Activité publiée le 26 02 2021
Dernière modification : 24 01 2022
Auteur : Andjekel
Sources : ows. h. et NSI4NOOBS